Are you still struggling on how to solve systems of linear equations? Would you like to learn how to do these techniques at your own pace?
Welcome! You have come to the right page. Here, I am going to reveal to you the step by step ways of Solving Systems of Linear Equations in Two Variables using the three different methods. I have included video tutorials from fellow educators that can help you understand the steps at your own pace.
I recommend that you Click Play and Pause the Videos until the are fully streamlined so you would be able to view them continuously. I have included also some links of other pages that will guide you through in mastering the techniques of solving systems of linear equations.
You maybe asking yourself, when will we use this?
By knowing how to solve these systems of linear equations in general, you will be able to solve real life problems related to it like time or money which is often one of the things we don't seem to have enough of.
Once you have these knowledge, you are ready to go. So, let's go ahead and look at systems in general to get us ready for the word problems that are ahead of us.
System of Linear Equations
A system of linear equations is two or more linear equations that are being solved simultaneously.
In this tutorial, we will be looking at systems that have only two linear equations and two unknowns.
Solution of a System
In general, a solution of a system in two variables is an ordered pair that makes BOTH equations true.
In other words, it is where the two graphs intersect, what they have in common. So if an ordered pair is a solution to one equation, but not the other, then it is NOT a solution to the system.
A consistent system is a system that has at least one solution.
An inconsistent system is a system that has no solution.
The equations of a system are dependent if ALL the solutions of one equation are also solutions of the other equation. In other words, they end up being the same line.
The equations of a system are independent if they do not share ALL solutions. They can have one point in common, just not all of them.
| There are three possible outcomes that you may encounter when working with these systems: |
| One Solution If the system in two variables has one solution, it is an ordered pair that is a solution to BOTH equations. In other words, when you plug in the values of the ordered pair it makes BOTH equations TRUE. If you do get one solution for your final answer, is this system consistent or inconsistent? If you said consistent, give yourself a pat on the back! If you do get one solution for your final answer, would the equations be dependent or independent? If you said independent, you are correct! The graph below illustrates a system of two equations and two unknowns that has one solution: 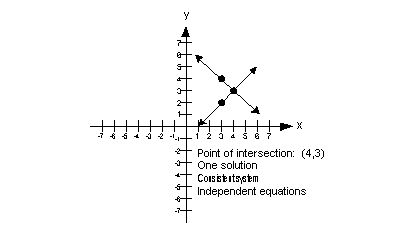 |
| No Solution If the two lines are parallel to each other, they will never intersect. This means they do not have any points in common. In this situation, you would have no solution. If you get no solution for your final answer, is this system consistent or inconsistent? If you said inconsistent, you are right! If you get no solution for your final answer, would the equations be dependent or independent? If you said independent, you are correct! The graph below illustrates a system of two equations and two unknowns that has no solution: 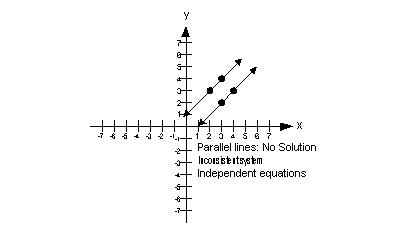 |
| Infinite Solutions If the two lines end up lying on top of each other, then there is an infinite number of solutions. In this situation, they would end up being the same line, so any solution that would work in one equation is going to work in the other. If you get an infinite number of solutions for your final answer, is this system consistent or inconsistent? If you said consistent, you are right! If you get an infinite number of solutions for your final answer, would the equations be dependent or independent? If you said dependent, you are correct! The graph below illustrates a system of two equations and two unknowns that has an infinite number of solutions: 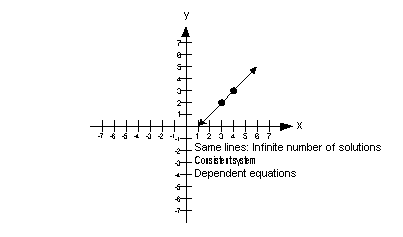 |
 Example 1: Determine whether each ordered pair is a solution of the system. Example 1: Determine whether each ordered pair is a solution of the system. |
| Let’s check the ordered pair (3, -1) in the first equation: |
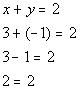 | *Plug in 3 for x and -1 for y *True statement |
| So far so good, (3, -1) is a solution to the first equation x + y = 2. Now, let’s check (3, -1) in the second equation: |
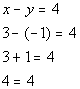 | *Plug in 3 for x and -1 for y *True statement |
| Hey, we ended up with another true statement, which means (3, -1) is also a solution to the second equation x - y = 4. Here is the big question, is (3, -1) a solution to the given system????? Since it was a solution to BOTH equations in the system, then it is a solution to the overall system. Now let’s put (0, 2) into the first equation: |
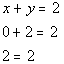 | *Plug in 0 for x and 2 for y *True statement |
| This is a true statement, so (0, 2) is a solution to the first equation x + y = 2. Finally, let’s put (0,2) into the second equation: |
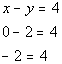 | *Plug in 0 for x and 2 for y *False statement |
This time we got a false statement, you know what that means. (0, 2) is NOT a solution to the second equation x - y = 4.
Here is the big question, is (0, 2) a solution to the given system?????
Since it was not a solution to BOTH equations in the system, then it is not a solution to the overall system.
Three Ways to
Solve Systems of Linear
Equations in Two Variables
Take a look at the following video tutorials on how to solve systems of linear equations.
(Note: Pause the videos until they are fully streamlined before viewing them in order for you to have continuous viewing.)
1. Solving Systems of Linear Equations by Graphing
2. Solving Systems of Linear Equations by Elimination Method
3. Solving Systems of Linear Equations by Substitution Method
Congratulations!
If you are still reading this, I believe you have already gone through all the video tutorials. Now, try this practice exercises. (Practice Problems will open in new window) Keep practicing and you will be master of these techniques of solving systems of linear equations. I hope these help.
Enjoy! ;-),
elizalde dao-anis
Recommended Sites:
http://themathgames.com/
https://www.yaymath.org/